呼和浩特市地方稅務局機關內設職能科室11個，監察室、機關黨委（機關紀委）、信息中心和國際稅收研究會黨團機構、紀檢監察部門、事業單位和社會團體各1個。同時設立派出機構12個，分別為：直屬征收管理一分局、直屬征收管理二分局、直屬征收管理三分局、直屬征收管理四分局、涉外征收管理分局、白塔空港物流園區分局、房地產稅收征收管理分局、社保分局、稽查局、金川經濟技術開發區地方稅務局、如意經濟開發區分局、金橋經濟技術開發區地方稅務局；直屬機構9個，分別為：新城區地方稅務局、回民區地方稅務局、玉泉區地方稅務局、賽罕區地方稅務局、土默特左旗地方稅務局、托克托縣地方稅務局、林格爾縣地方稅務局、清水河縣地方稅務局、武川縣地方稅務局。其中，派出機構副處級單位2個，正科級單位10個。直屬機構分別在9個旗縣（區）設地稅局，均為正科級規格。

隨著社會科技的不斷發展，為了取得更好的會議效果，一般的會議話筒在一些場合已經不太適用，轉而出現了新型的會議系統，這便是手拉手陣列式無咪桿會議系統，此類會議系統功能先進、超遠拾音、自動增益、無遮擋、高穩定性、強抗干擾能力，非常適應現代智能會議的需求。陣列式會議系統是將17只高性能全音域拾音頭，結合數字麥克風陣列技術，在頻率響應中根據時域中波束形成與空間濾波器相仿的應用，分析出接收到語音信號音源的方向以及其變化，這些分析都可以由極坐標圖以波束形式來顯示語音信號的強度與角度。內置數字電路激勵芯片，具備150°拾音角度，無論是坐姿還是站姿均能保證音質效果。

陣列會議系統工作原理

陣列式會議系統是一組位于空間不同位置的全向麥克風按一定的形狀規則布置形成的陣列，是對空間傳播聲音信號進行空間采樣的一種裝置，采集到的信號包含了其空間位置信息。根據聲源和麥克風陣列之間距離的遠近，可將陣列分為近場模型和遠場模型。根據陣列麥克風的拓撲結構，則可分為線性陣列、平面陣列、體陣列等。

一、近遠場模型

聲波是縱波，即媒質中質點沿傳播方向運動的波。聲波是一種振動波，聲源發聲振動后，聲源四周的媒質跟著振動，聲波隨著媒質向四周擴散，所以是球面波。

根據聲源和麥克風陣列距離的遠近，可將聲場模型分為兩種：近場模型和遠場模型。近場模型將聲波看成球面波，它考慮麥克風陣元接收信號間的幅度差；遠場模型則將聲波看成平面波，它忽略各陣元接收信號間的幅度差，近似認為各接收信號之間是簡單的時延關系。顯然遠場模型是對實際模型的簡化，極大地簡化了處理難度。一般語音增強方法就是基于遠場模型。

近場模型和遠場模型的劃分沒有絕對的標準，一般認為聲源離麥克風陣列中心參考點的距離遠大于信號波長時為遠場；反之，則為近場。設均勻線性陣列相鄰陣元之間的距離(又稱陣列孔徑)為d，聲源最高頻率語音的波長(即聲源的最小波長)為λmin，如果聲源到陣列中心的距離大于2d²/λ_min，則為遠場模型，否則為近場模型，如下圖所示：

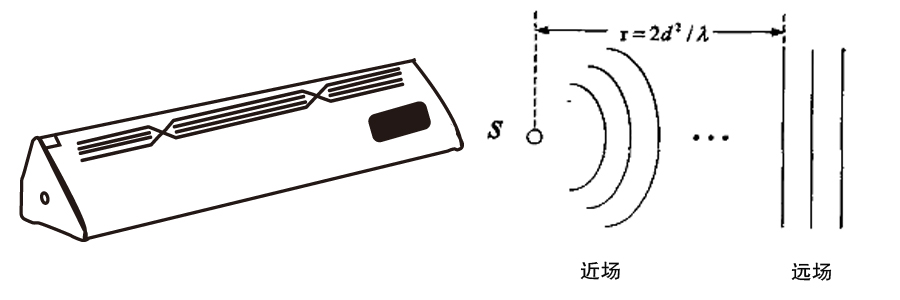
二、拓撲結構

按陣列麥克風的維數，可分為一維、二維和三維陣列麥克風。

一維陣列麥克風，即線性陣列麥克風，其陣元中心位于同一條直線上。根據相鄰陣元間距是否相同，又可分為均勻線性陣列(Uniform Linear Array，ULA)和嵌套線性陣列，如下圖所示。均勻線性陣列是最簡單的陣列拓撲結構，其陣元之間距離相等、相位及靈敏度一直。嵌套線性陣列則可看成幾組均勻線性陣列的疊加，是一類特殊的非均勻陣。線性陣列只能得到信號的水平方向角信息。

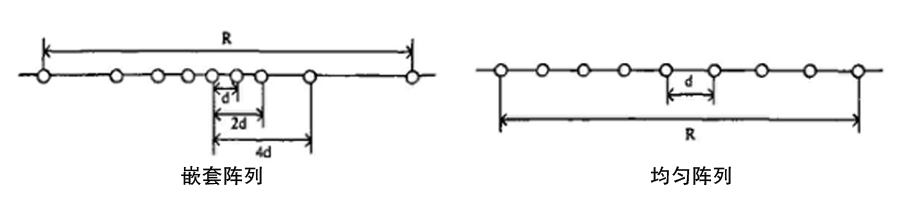
二維陣列麥克風，即平面陣列麥克風，其陣元中心分布在一個平面上。根據陣列的幾何形狀可分為等邊三角形陣、T型陣、均勻圓陣、均勻方陣、同軸圓陣、圓形或矩形面陣等，如下圖所示。平面陣列可以得到信號的水平方位角和垂直方位角信息。

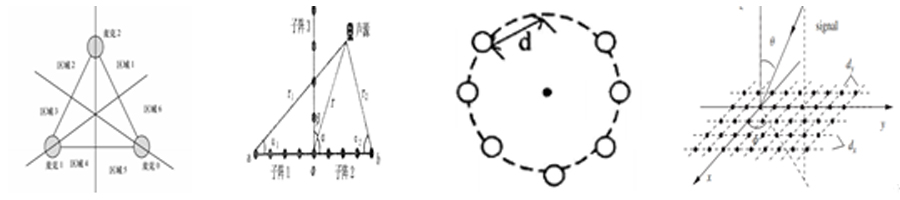
平面陣列拓撲結構

三維陣列麥克風，即立體陣列麥克風，其陣元中心分布在立體空間中。根據陣列的立體形狀可分為四面體陣、正方體陣、長方體陣、球型陣等，如下圖所示。立體陣列可以得到信號的水平方位角、垂直方位角和聲源與陣列麥克風參考點距離這三維信息。

立體陣列拓撲結構

三、波束形成

波束形成，是對各陣元的輸出進行時延或相位補償、幅度加權處理，以形成指向特定方向的波束。

在遠場模型中，假設輸入是一個平面波。設傳播方向為θ，時域頻率(弧度)為ω，聲音在介質中的傳播速度為c，對于在一個局部均勻的介質里傳播的平面波，定義波束k為k = ωsinθ/c = 2sinθ/λ，其中λ是對應于頻率ω的波長。由于信號到達不同的傳感器的時間不同，則陣列接收到的信號可表示為 f(t)=[f(t-τ₀) f(t-τ₁)…f(t-τ_N-1)]^T=[exp(jω(t-kτ₀)) exp(jω(t-kτ₁))…exp(jω(t-kτ_N-1))]^T

其中τ_n為第n個陣元接收到的信號相對于參考點的時延，N為陣元個數，T表示轉置。

定義v(k) = [e^-jωkτ0 e^-jωkτ1 …e^-jωkτN-1]^T

矢量v包含了陣列的空間特征，稱為陣列流行矢量。則f(t)可表示為f(t) = ejωtv(k)。

陣列處理器對一個平面波的響應為y(t,k) =HT(ω) v(k)ejωt

其中H(ω)是濾波器系數向量的傅里葉變換。符號y(t,k)強調了輸出和輸入波數k的關系。時域上的相關性體現在輸出是一個復指數，和輸入平面波有相同的頻率。在頻域上式可表示為Y(ω,k) =H^T(ω) v(k)。

注意此處ω對應單一的輸入頻率，所以是窄帶的。陣列的空時處理關系完全可以由上式的右端描述，稱為陣列的頻率-波數響應函數。它描述了一個陣列對于時域頻率為ω，波數為k的輸入平面波的復增益。

陣列的波束方向圖反映了平面波在一個局部均勻的介質中傳播情況，它是用入射方向表示的頻率-波數響應函數，可以寫成B(ω:θ) = Y(ω,k)|_k=sinθ。

陣列的波束方向圖是確定陣列性能的關鍵要素，其主要參數有3dB帶寬，到第一零點的距離，第一旁瓣高度，旁瓣衰減速度等。其幅度的平方定義為功率方向圖，是常用的一種陣列性能度量。

四、時延補償

由于麥克風陣元空間位置的差異，各陣元接收到的信號存在時延，在對信號處理之前進行時延補償，保證各陣元待處理數據的一致性，使陣列指向期望方向。 考慮最簡單的均勻線性麥克風陣列，如下圖所示：

設陣列麥克風共用M個陣元，中心為參考點，陣元間距為d，信號入射角為θ，聲音傳播速度為c，則根據幾何知識，第m(0≤m≤M-1)個陣元的時延為τ_m = (d/c) sinθ(m-(K-1)/2)。

麥克風采集的是數字信號，設采樣周期為T，則對時域離散的信號來說，時延為D = τ/T。

通常D不是一個整數，而對離散信號來說，整數時延才有意義。對于非整數D，可以分解為整數部分和分數部分D = ⌊D⌋ + d，式中，⌊D⌋為D的向下取整，0≤d<1。對于非零的分數部分d，此時信號實際值介于兩個相鄰采樣點之間，即分數延遲。在實際處理中，可對d四舍五入取整，然后加上⌊D⌋，得到近似整數時延，但這種方法處理的結果不夠精確。

為了得到較為精確的處理結果，就必須設計分數時延濾波器，對采樣信號進行精確的時延補償。理想的分數時延濾波器的沖激響應可表示為h_id(m) = sinc(m-D)。

由數字信號處理知識可知，上式是無限長、非因果不穩定的，在物理上不可實現。為了解決這一問題，在實際操作中，通常會對上式進行加窗，加窗后濾波器的沖激響應為h(m)=(W(m-D)sinc(m-D), 0≤m≤M-1。加窗后的分數時延濾波器的時延精確程度與理想分數時延濾波器非常接近。